Suku ke-5 dan suku ke-9 sebuah barisan geometri dengan rasio positif berturut-turut 12 dan 48. Jumlah 12 suku pertama barisan tersebut adalah
Suku ke-5 dan suku ke-9 sebuah barisan geometri dengan rasio positif berturut-turut 12 dan 48. Jumlah 12 suku pertama barisan tersebut adalah . . . .
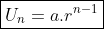
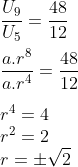
^{4}=12\\\\a\times&space;4=12\\\\a=\frac{12}{4}\\\\a=3 "\\a.r^{4}=12\\\\a.(\sqrt{2})^{4}=12\\\\a\times 4=12\\\\a=\frac{12}{4}\\\\a=3")
}{r-1}\\\\S_{n}=\frac{3((\sqrt{2})^{12}-1)}{\sqrt{2}-1}\\\\S_{n}=\frac{3(64-1)}{\sqrt{2}-1}\\\\S_{n}=\frac{3(63)}{\sqrt{2}-1}\\\\S_{n}=\frac{189}{\sqrt{2}-1}\\\\S_{n}=\frac{189}{\sqrt{2}-1}\times&space;\frac{\sqrt{2}+1}{\sqrt{2}+1}\\\\S_{n}=\frac{189(\sqrt{2}+1)}{2-1}\\\\S_{n}=189(\sqrt{2}+1) "\\S_{n}=\frac{a(r^{n}-1)}{r-1}\\\\S_{n}=\frac{3((\sqrt{2})^{12}-1)}{\sqrt{2}-1}\\\\S_{n}=\frac{3(64-1)}{\sqrt{2}-1}\\\\S_{n}=\frac{3(63)}{\sqrt{2}-1}\\\\S_{n}=\frac{189}{\sqrt{2}-1}\\\\S_{n}=\frac{189}{\sqrt{2}-1}\times \frac{\sqrt{2}+1}{\sqrt{2}+1}\\\\S_{n}=\frac{189(\sqrt{2}+1)}{2-1}\\\\S_{n}=189(\sqrt{2}+1)")
A. 12(√2 + 1)
B. 63(√2 + 1)
C. 93(√2 + 1)
D. 189(√2 + 1)
E. 381(√2 + 1)
Pembahasaan :
Diketahui :
Suku ke-5 = 12
U5 = 12
Suku ke-9 = 48
U9 = 49
Ditanyakan :
Jumlah 12 suku pertama barisan tersebut adalah . . . .?
Jawab :
Ingat rumus suku ke-n barisan geometri adalah :
Sehingga dapat kita peroleh untuk perbandingannya :
Oleh karena rasio positif, maka kita ambil nilai r = √2
Kita subsitusikan nilai r = √2 ke rumus U5,
maka diperoleh :
Kemudian kita subsitusikan nilai a = 3 dan r = √2
ke dalam rumus S12, maka diperoleh :
Jadi, Jumlah 12 suku pertama barisan
tersebut adalah 189(√2 + 1)
Jawabannya ( D )
Itulah pembahasan contoh soal mengenai materi barisan geometri yang diambil dari Buku MATEMATIKA SMA/SMK/Se-derajat. Semoga bermanfaat dan mudah untuk dipahami ya. Tetap semangat semuannya . . . . . .
0 Response to "Suku ke-5 dan suku ke-9 sebuah barisan geometri dengan rasio positif berturut-turut 12 dan 48. Jumlah 12 suku pertama barisan tersebut adalah"
Post a Comment