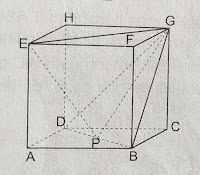
Kubus ABCD.EFGH mempunyai panjang rusuk 8 cm. Jarak titik E ke bidang BGD adalah...
Kubus ABCD.EFGH mempunyai panjang rusuk 8 cm. Jarak titik E ke bidang BGD adalah...

A. 1/3 √3 cm
B. 2/3 √3 cm
C. 4/3 √3 cm
D. 8/3 √3 cm
E. 16/3 √3 cm
Pembahasan :
Diketahui : panjang rusuk 8 cm
Ditanyakan : Jarak titik E ke bidang BGD adalah...?
Jawab :
*Kita ilustrasikan soal kedalam bentuk gambar.

* Jarak titik E ke bidang BGD sama dengan jarak titik E ke garis GP dengan titik tengah BD yaitu sama dengan panjang EQ.
*EG dan AC merupakan diagonal sisi maka,
panjang EG = AC = √(EP² + FG²)
= √(8² + 8²)
= √(64 + 64)
= √128
= √(64 x 2)
= 8√2 cm
* Kita mencari panjang AP.
AP = 1/2 (AC)
= 1/ 2 (8√2)
= 4√2 cm
* Karena segitiga APE siku-siku di A. Maka :
AE = 8 cm
AP = 4√2 cm
EP = √(AE² + AP²)
= √(8² + (4√2)²)
= √(64 + (16.2))
= √(64 + 32)
= √96
= √(16 x 6)
= 4√6 cm
* Perhatikan segitiga EGP.

GP = EP = 4√6 cm
PQ = x cm
maka :
GQ = (4√6 - x) cm
Sehingga :
EQ² = EP² - PQ² = EG² - GQ²
(4√6)² - x² = (8√2)² - (4√6 - x)²
(16.6) - x² = (64.2) - ((16.6) - 2.(4√6).x + x²
96 - x² = 128 - (96 - 8√6x + x²)
96 - x² = 128 - 96 + 8√6x - x²
96 = 32 + 8√6x
96 - 32 = 8√6x
64 = 8√6x
64 / 8√6 = x
8/6 √6 = x
4/3 √6 = x
Sehingga di peroleh panjang
PQ = 4/3 √6 cm
Selanjutnya kita akan mencari nilai EQ.
EQ = √(EP² - EQ²)
= √((4√6)² - (4/3 √6)²)
= √ (96 - 32/3)
= √(256/3)
= 16/3 √3 cm.
Jadi, Jarak titik E ke bidang BGD adalah 16/3 √3 cm.. Jawabannya ( E ).
Itulah pembahasan soal mengenai bangun ruang kubus untuk SMA/SMK/MA yang mimin ambil dari soal soal latihan UNBK. Semoga bermanfaat dan mudah untuk dipahami. Tetap semangat temen-temen. selalu berdoa yahhh. Terima kasihh semuaaa...
0 Response to "Kubus ABCD.EFGH mempunyai panjang rusuk 8 cm. Jarak titik E ke bidang BGD adalah..."
Post a Comment