Diketahui kubus ABCD.EFGH dengan Panjang rusuk 6 cm. Jarak titik E ke bidang AFH adalah

Diketahui kubus ABCD.EFGH dengan Panjang rusuk 6 cm. Jarak titik E ke bidang AFH adalah . . .

A. 4√3

B. 4√2

C. 3√3

D. 3√2

E. 2√3

Pembahasaan :

Diketahui :

Panjang rusuk kubus adalah 6 cm

Ditanyakan :

Jarak titik E ke bidang AFH adalah . . . ?

Jawab :

Agar lebih mudah, kita gambar terlebih dahulu bentuk kubus sesuai dengan poin yang ada pada soal.

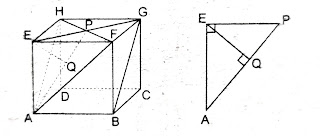
Dari gambar di atas, dapat kita ketahui bahwa :

Jarak titik E ke bidang AFH = Panjang EQ

EQ adalah jarak titik E ke garis AP denga P titik tengah EG.

EG adalah diagonal sisi 

Panjang EG adalah :

EG = √(EF² + FG²)

      = √(6² + 6²)

      = √(36 + 36)

      = √72

      = √( 36 x 2 )

      = 6√2

Panjang AE   = 6 cm

Panjang EP   = ½ EG

                     = ½ x 6√2

                     = 3√2 cm

Karena segitiga AEP siku-siku di E, maka :

AP = √(AE² + EP²)

      = √(6² + (3√2)²)

      = √(36 + 18)

      = √54

      = √(9 x 6)

      = 3√6 cm

Karena segitiga AEP siku-siku di E. Maka luas segitiga AEP dapat dirumuskan sebagai berikut :

L = ½ x AP x EQ

Atau

L = ½ x AE x EP

Dari kedua rumus luas segitiga AEP di atas dapat kita peroleh yaitu :

½ x AP x EQ = ½ x AE x EP

½ x 3√6 x EQ = ½ x 6 x 3√2

EQ = (6 x 3√2) / 3√6

EQ = (6/√3) x (√3/√3)

EQ = 6/3 √3

EQ = 2√3 cm

Jadi, Jarak titik E ke bidang AFH adalah 2√3 cm

Jawabannya ( E )

Itulah pembahasan soal tentang materi Bangun Ruang Sisi Datar atau bangun Kubus. Semoga bermanfaat dan mudah untuk dipahami yah temen temen. Jika ada yang ingin ditanyakan silahakan tinggalkan pesan di kolom komentar. Teruslah berproses hingga hasil tak menjadi tujuan utama Kembali. Terima kasih semua . . .

Advertisement

Subscribe to receive free email updates: