Keuntungan seorang pedagang bertambah setiap bulan dengan jumlah yang sama. Keuntungan sampai bulan ke empat Rp.215.000,00 dan sampai bulan ke delapan Rp.470.000,00. Jumlah keuntungan sampai bulan kedua belas adalah
Keuntungan seorang pedagang bertambah setiap bulan dengan jumlah yang sama. Keuntungan sampai bulan ke empat Rp.215.000,00 dan sampai bulan ke delapan Rp.470.000,00. Jumlah keuntungan sampai bulan kedua belas adalah . . .
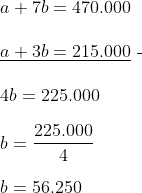
A. Rp. 1.012.500,00
B. Rp. 927.500,00
C. Rp. 845.000,00
D. Rp.665.000,00
E. Rp. 687.000,00
Pembahasan :
Diketahui :
Keuntungan bulan ke-4 = Rp.215.000,00
Keuntungan bulan ke-8 = Rp.470.000,00
Jumlah keuntungan membentuk deret aritmatika.
Ditanyakan : Jumlah keuntungan sampai bulan kedua belas adalah . . .?
Jawab :
Kita ubah soal ke dalam model matematika.
Karena jumlah keuntungan pedagang itu membentuk deret aritmatika, maka :
Un = a + (n - 1)b
Untuk Keuntungan bulan ke-4
Un = a + (n - 1)b
U4 = a + (4 - 1)b
215.000 = a + 3b
a + 3b = 215.000 . . .persamaan (1)
Untuk keuntungan bulan ke-8
Un = a + (n - 1)b
U8 = a + (8 - 1)b
470.000 = a + 7b
a + 7b = 470.000 . . .persamaan (2)
Selanjutnya kita eliminasi persamaan (1) dan (2)
Selanjutnya kita subsitusikan nilai b = 56.250 ke persamaan (1)
a + 3b = 215.000
a + 3(56.250) = 215.000
a + 168.750 = 215.000
a = 215.000 - 168.750
a = 46.250
Sehingga jumlah keuntungan bulan ke-12 adalah :
Un = a + (n - 1)b
U12 = 46.250 + (12 - 1)56.250
= 46.250 + (11)56.250
= 46.250 + 618.750
= 665.000
Jadi, Jumlah keuntungan sampai bulan kedua belas adalah Rp.665.000,00
Jawabannya ( D ).
Itulah pembahasan contoh soal aplikasi mengenai materi barisan dan deret aritmatika. Semoga bermanfaat dan mudah untuk dipahami yah, jangan lupa untuk selalu bahagia. Terima kasihh...
0 Response to "Keuntungan seorang pedagang bertambah setiap bulan dengan jumlah yang sama. Keuntungan sampai bulan ke empat Rp.215.000,00 dan sampai bulan ke delapan Rp.470.000,00. Jumlah keuntungan sampai bulan kedua belas adalah"
Post a Comment