Bentuk akar : Sifat dan cara merasionalkan lengkap dengan contoh soal
A. Pengertian Bentuk Akar

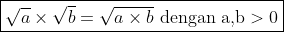
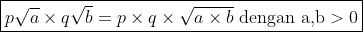
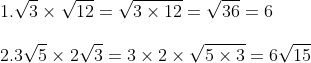



\sqrt{c}})
\sqrt{c}})
\sqrt{3}=7\sqrt{3}\\\\2.&space;6\sqrt{2}-&space;4\sqrt{2}=(6-4)\sqrt{2}=2\sqrt{2}\end{align})
![\boxed{(\sqrt[m]{a})^{2}=\sqrt[m]{a}\times \sqrt[m]{a}}](https://latex.codecogs.com/gif.latex?\boxed{(\sqrt[m]{a})^{2}=\sqrt[m]{a}\times&space;\sqrt[m]{a}})
^{2}=a^{2}+2a\sqrt{b}+(\sqrt{b})^{2}})
^{2}=(\sqrt{a})^{2}-2(\sqrt{a})(\sqrt{b})+(\sqrt{b})^{2}})
![\\1.(\sqrt[3]{5})^{2}=\sqrt[3]{5}\times \sqrt[3]{5}=\sqrt[3]{25}\\\\2.(2+\sqrt{3})^{2}=2^{2}+2.2.\sqrt{3}+(\sqrt{3})^{2}](https://latex.codecogs.com/gif.latex?\\1.(\sqrt[3]{5})^{2}=\sqrt[3]{5}\times&space;\sqrt[3]{5}=\sqrt[3]{25}\\\\2.(2+\sqrt{3})^{2}=2^{2}+2.2.\sqrt{3}+(\sqrt{3})^{2})
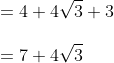
^{2}=(\sqrt{3})^{2}-2.\sqrt{3}.\sqrt{5}+(\sqrt{5})^{2})
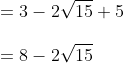

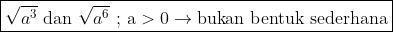




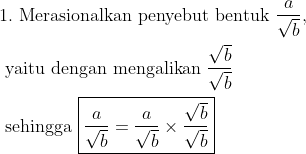
}{2}=4\sqrt{2})


}{9-5}\\\\=\frac{4(3-\sqrt{5})}{4}\\\\=3-\sqrt{5})
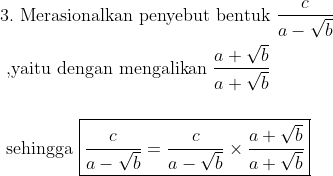
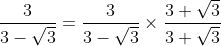
}{9-3}\\\\=\frac{3(3+\sqrt{3})}{6}\\\\=\frac{1}{2}(3+\sqrt{3}))
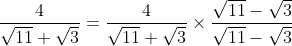
}{11-3}\\\\=\frac{4(\sqrt{11}-\sqrt{3})}{8}\\\\=\frac{1}{2}(\sqrt{11}-\sqrt{3}))

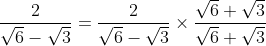
}{6-3}\\\\=\frac{2(\sqrt{6}+\sqrt{3})}{3}\\\\=\frac{2}{3}(\sqrt{6}+\sqrt{3}))
![\boxed{a=p^{\frac{1}{n}}=\sqrt[n]{p}}](https://latex.codecogs.com/gif.latex?\boxed{a=p^{\frac{1}{n}}=\sqrt[n]{p}})
^{\frac{1}{n}}=p^{\frac{1}{m\times&space;n}}})
![b\text{ . }\boxed{p^{\frac{m}{n}}=p^{m\times \frac{1}{n}}=(p^{m})^{\frac{1}{n}}=\sqrt[n]{p^{m}}}](https://latex.codecogs.com/gif.latex?b\text{&space;.&space;}\boxed{p^{\frac{m}{n}}=p^{m\times&space;\frac{1}{n}}=(p^{m})^{\frac{1}{n}}=\sqrt[n]{p^{m}}})
![c\text{ . }\boxed{p^{\frac{m}{n}}=p^{\frac{1}{n}\times m}=\left ( p^{\frac{1}{n}} \right )^{m}=(\sqrt[n]{p})^{m}}](https://latex.codecogs.com/gif.latex?c\text{&space;.&space;}\boxed{p^{\frac{m}{n}}=p^{\frac{1}{n}\times&space;m}=\left&space;(&space;p^{\frac{1}{n}}&space;\right&space;)^{m}=(\sqrt[n]{p})^{m}})


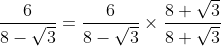
}{64-3}\\\\=\frac{6(8+\sqrt{3})}{61}\\\\=\frac{6}{61}(8+\sqrt{3}))
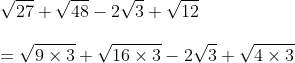

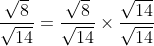
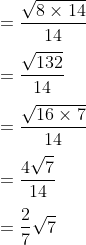
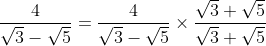
}{3-5}\\\\=\frac{4(\sqrt{3}+\sqrt{5})}{-2}\\\\=-2(\sqrt{3}+\sqrt{5})\\\\=-2\sqrt{3}-2\sqrt{5})
Pada dasarnya bentuk akar merupakan kebalikan dari bentuk bilangan berpangkat. Bentuk akar sendiri merupakan akar dari suatu bilangan yang hasilnya bukan bilangan rasional maupun merupakan bilangan irasional.

Bentuk akar sendiri bisa dikatakan bentuk suatu bilangan irasional karena tidak dapat dinyatakan dalam bentuk a/b, a dan b, a,b merupakan bilangan bulat tidak sama dengan 0.
Bilangan bentuk akar sendiri sering identik berada di dalam tanda "√." yaitu disebut tanda akar. Contoh dari bilangan bentuk akar sendiri yaitu √2, √5, √14, dan lain sebagainya. Sedangkan bentuk akar √25 merupakan bukan bentuk akar karena bilangan itu masih bisa disederhanakan.
Seperti halnya dengan bentuk bilangan berpangkat, bilangan bentuk akar sendiri juga memiliki sifat-sifatnya tersendiri. Berikut merupakan sifat-sifat dari bentuk akar.
1. Sifat perkalian bentuk akar
Untuk mengalikan bentuk akar dapat dilakukan dengan sifat berikut :
Contohnya :
2. Sifat pembagian bentuk akar
Untuk membagikan bentuk akar dapat dilakukan dengan sifat berikut :
Contohnya :
3. Sifat penjumlahan dan pengurangan bentuk akar
Untuk menjumlahkan atau mengurangkan bentuk
akar kita bisa melakukang dengan sifat berikut :
Contohnya :
4. Sifat perpangkatan bilangan bentuk akar
Untuk memangkatkan bentuk akar, kita
bisa menggunakan sifat berikut :
Contohnya :
Itulah 4 sifat bentuk akar yang perlu temen-temen pahami, ketika kita paham akan konsep ke empat sifat itu, insyaalloh kita akan mudah mengerjkan tipe-tipe soal bentuk akar pada saat ujian nanti.
B. Merasionalkan Bentuk Akar
Seringkali kita bingung ketika akan mencari suatu nilai paling sederhana pada soal bentuk akar, nilai paling sederhana bentuk akar tersebut bisa kita cari dengan merasionalkan bentuk akarnya.
Bagaimana sih cara merasionalkan bentuk akar tersebut? Nah sebelum ke sana kita harus tahu apa saja syarat-syarat yang memenuhi bentuk akar agar bisa dirasionalkan.
Berikut merupakan syarat dan ketentuan bentuk akar supaya bisa kita rasionalkan :
1. Tidak memuat faktor yang pangkatnya lebih dari satu
Contohnya :
2 Tidak ada bentuk akar pada penyebut
Contohnya :
3. Tidak mengandung pecahan
Contohnya :
Ketiga syarat itu merupakan suatu ketentuan yang menyebutkan apakah suatu bentuk akar itu sudah rasional ataupun tidak. Jadi kita harus tahu betul ketika ada suatu soal apakah bentuk akar itu sudah paling sederhana(rasional) ataupun tidak.
C. Cara Merasionalkan Suatu Pecahan Bentuk Akar
Selain sifat bentuk akar dan syarat merasionalkan bentuk akar, selanjutnya kita akan belajar bagaimana cara merasionalkan bentuk akar itu sendiri.
Apa sih itu merasionalkan bentuk akar ? Merasionalkan bentuk akar pada dasarnya merupakan merasionalkan bentuk penyebut pecahan dengan mengubahnya menjadi bentuk bilangan yang rasional.
Cara merasionalkan setiap penyebut pecahan bentuk akar itu berbeda-beda, ada yang dengan cara mengalikan penyebut-penyebut tersebut dengan pasangan bentuk akar sekawannya sehingga diperoleh penyebut bilangan rasional.
Berikut merupakan cara merasionalkan penyebut suatu pecahan bentuk akar :
Contohnya :
Contohnya :
Contohnya :
Contohnya :
Contohnya :
D. Pangkat Pecahan
Jika a..= p dengan a dan p adalah bilangan real
dan n adalah bilangan bulat, dengan n > 0, maka
Secara umum bilangan berpangkat pecahan memiliki sifat yang berlaku sebagai berikut :
Contoh soal latihan :
1. Bentuk sederhana dari  adalah...
adalah...
Jawab :
2. Bentuk rasional dari 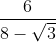 adalah...
adalah...
Jawab :
3. Bentuk sederhana dari adalah...
Jawab :
4. Bentuk sederhana dari 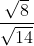 adalah...
adalah...
Jawab :
5. Bentuk sederhana dari 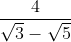 adalah...
adalah...
Jawab :
Setelah kita mengetahui sifat-sifat bentuk akar, syarat untuk merasionalkan bentuk akar, dan cara bagaimana merasionalkan bentuk akar, serta sifat -sifat pangkat pecahan. Diharapkan temen-temen semua bisa dengan mudah memahami materi bentuk akar kali ini.
Semoga bermanfaat dan Sukses selalu. Jika ada yang ditanyakan atau didiskusikan perihal materi bentuk akar kali ini, silahkan tinggalkan pesan di kolom komentar. Salam hangat dari mimin.
0 Response to "Bentuk akar : Sifat dan cara merasionalkan lengkap dengan contoh soal"
Post a Comment