10 contoh soal & pembahasan perbandingan senilai dan perbandingan berbalik nilai
Soal perbandingan seniali dan perbandingan berbalik nilai seringkali kita temui pada setiap sisi kehidupan, dan fenomena-fenomena itu bisa kita kaji dan telusuri dengan kemampuan logika kita, seperti dengan konsep perbandingan.

Berikut merupakan contoh soal dan pembahasan materi perbandingan senilai dan perbandingan berbalik nilai yang mimin ambil pada buku ajar matematika SMP kelas 9.
A. 22 meter
B. 21 meter
C. 18 meter
D. 15 meter
Pembahasan :
Diketahui :
|
Jarak ( meter ) |
Banyak putaran |
|
27 |
18 |
|
x |
12 |
Jawab :
Note : Semakin sedikit putaran roda, maka semakin sedikit pula jarak yang ditempuh.
Sehingga kita menggunakan rumus perbandingan senilai.
Jadi, jarak yang ditempuh roda setelah 12 kali putaran adalah 18 meter. Jawabannya ( C ).
2. Persediaan makanan untuk 50 orang cukup 18 hari. Jika ditambahkan 10 orang, maka berapa lama persediaan makanan akan tercukupi...?
A. 13
B. 15
C. 17
D. 19
Pembahasan :
Diketahui : Banyak pekerja setelah ditambah = 50+10 = 60 orang, , maka
|
Banyak orang |
Waktu ( hari ) |
|
50 |
18 |
|
60 |
x |
Jawab :
Note : Semakin banyak orang, maka semakin cepat pula persediaan makanan itu habis.
Sehingga kita menggunakan rumus perbandingan berbalik nilai.
Jadi, lama persediaan makanan itu akan tercukuoi selama 15 hari. Jawabannya ( B ).
3. Persegi panjang P berukuran panjang 12 cm dan lebar 6 cm, sedengkan persegi panjang Q berukuran panjang 28 cm dan lebar 8 cm. Perbandingan keliling kedua persegi panjang adalah...?
A. 2 : 1
B. 1 : 4
C. 1 : 3
D. 1 : 2
Pembahasan :
Diketahui :
|
|
Panjang ( cm ) |
Lebar ( cm ) |
|
Persegi
Panjang P |
12 |
6 |
|
Persegi
Panjang Q |
28 |
8 |
Jawab :
Note : Kita cari terlebih dahulu masing-masing dari keliling persegi panjang P dan Q.
*Keliling persegi panjang P = 2 (p+l)
= 2 ( 12 + 6)
= 2 ( 18 )
= 36 cm
*Keliling persegi panjang Q = 2 (p+l)
= 2 ( 28 + 8 )
= 2 ( 36 )
= 72 cm
*Perbandingan keliling persegi panjang = K.persegi panjang P : K.persegi panjang Q
= 36 : 72
= 1 : 2
Jadi, Perbandingan keliling kedua persegi panjang adalah 1 : 2. Jawabannya ( D ).
4. Segitiga A berukuran tinggi 10 cm dan alas 6 cm. Segitiga B berukuran tinggi 30 cm dan alas 8 cm. Perbandingan kedua segitiga adalah...
A. 1 : 2
B. 2 : 1
C. 4 : 1
D. 1 : 4
Pembahasan :
Diketahui :
|
|
Tinggi |
Alas |
|
Segitiga
A |
10 |
6 |
|
Segitiga
B |
30 |
8 |
Jawab :
Note : Kita cari terlebih dahulu luas masing-masing kedua segitiga A dan B.
*Luas segitiga A = 1/2 x a x t
= 1/2 x 6 x 10
= 3 x 10
= 30 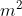
*Luas segitiga B = 1/2 x a x t
= 1/2 x 8 x 30
= 4 x 30
= 120 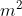
Perbandingan Luas segitiga = L.Segitiga A : L.segitiga B
= 30 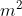 : 120
: 120 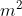
= 1 : 4
Jadi, perbandingan luas segitiga A dan B adalah 1 : 4. Jawabannya ( D ).
5. Sebuah mobil memerlukan 3 liter bensin untuk menempuh jarak 45 km. Jarak yang ditempuh mobil itu jika menghabiskan 40 liter bensin adalah...?
A. 550 km
B. 600 km
C. 700 km
D. 750 km
Pembahasan :
Diketahui :
|
Bensin ( liter ) |
Jarak
( km ) |
|
3 |
45 |
|
40 |
x |
Jawab :
Note : Semakin banyak bensin yang ada, maka semakin jauh pula jarak tempuh mobil tersebut.
Sehingga kita menggunakan rumus perbandingan senilai.
Jadi, jarak tempuh mobil dengan 45 liter bensin adalah 600 km. Jawabannya ( B ).
6. Seorang petani mempunyai persediaan makanan untuk 80 ekor ayam selama 25 hari. Jika petani itu membeli 20 ekor ayam lagi, maka persediaan makanan itu akan habis dalam...hari.
A. 30
B. 10
C. 20
D. 15
Pembahasan :
Diketahui : Banyak ayam setelah membeli 20 ekor = 80 + 20 = 100 ekor
|
Banyak ayam |
Waktu
( hari ) |
|
80 |
25 |
|
100 |
x |
Jawab :
Note : Semakin banyak ekor ayam, maka semakin cepat pula persediaan makanan itu akan habis.
Sehingga kita menggunakan rumus perbandingan berbalik nilai.
Jadi, lama persediaan makanan itu akan habis dalam 20 hari. Jawabannya ( C ).
7. Suatu pekerjaan dapat diselesaikan oleh 10 orang dalam 21 hari. Setelah 3 hari bekerja , Pekerjaan itu terhenti selama 3 hari. Agar pekerjaan tersebut dapat diselesaikan tepat waktu, banyak pekerja yang perlu ditambah adalah...
A. 2 pekerja
B. 5 pekerja
C. 10 pekerja
D. 7 pekerja
Pembahasan :
Diketahui :
Note : Bacalah soal dengan seksama. Pekerjaan itu dikerjakan 10 orang akan selesai selama 21 hari. Karena setelah
dikerjakan 3 hari maka sisa waktu pengerjaannya 18 hari lagi oleh 10 orang pekerja.
Tetapi pekerjaan itu dihentikan selama 3 hari, maka sisa waktu pengerjaannya
tinggal 15 hari. Agar pengerjaan itu tepat waktu, maka memerlukan
tambahan pekerja. Jika ditulis dalam bentuk tabel adalah sebagai berikut :
|
Pekerja |
Waktu
(Hari ) |
|
10 |
21 |
|
10 |
21-3 = 18 |
|
x |
21-3-3 =15 |
Jawab :
Note : Semakin sedikit waktu yang tersedia, maka semakin banyak pula pekerja yang dibutuhkan.
Sehingga kita menggunakan rumus perbandingan berbalik nilai.
Jadi, tambahan pekerja yang diperlukan = 12 -10 = 2 pekerja. Jawabannya ( A )
8. Jarak kta A ke kota B jika ditempuh dengan kereta api berkecepatan 120 km/jam memerlukan waktu 3 jam. Waktu yang diperlukan untuk menempuh jarak tersebut jika digunakan mobil dengan kecepatan 90 km/jam adalah x, maka nilai x adalah...?
A. 4 jam
B. 6 jam
C. 5 jam
D. 7 jam
Pembahasan :
Diketahui :
|
Kecepatan ( km/jam ) |
Waktu
( jam ) |
|
140 |
3 |
|
90 |
x |
Jawab :
Note : Semakin lambat kecepatan mobil, maka semakin lama waktu yang diperlukan.
Sehingga kita menggunakan rumus perbandingan berbalik nilai.
Jadi, waktu yang diperlukan oleh moobil dengan kecepatan 90 km/jam adalah 4 jam. Jawabannya ( A ).
9. Jika 20 orang dapat menyelesaikan pembangunan rumah dalam waktu 60 hari, setelah 12 hari bekerja, pekerjaan terhenti selama 8 hari. Tambahan pekerja yang diperlukan agar pekerjaan tepat waktu adalah...
A. 4
B. 24
C. 44
D. 54
Pembahasan :
Diketahui :
Note : Bacalah soal dengan seksama. Pembangunan rumah itu dikerjakan oleh 20 orang akan selesai selama 60 hari. Karena setelah
dikerjakan selama 12 hari maka sisa waktu pengerjaannya 48 hari lagi oleh 20 pekerja.
Tetapi pekerjaan itu diliburkan selama 8 hari, maka sisa waktu pengerjaannya
tinggal 40 hari. Agar pembangunan rumah itu tepat waktu, maka memerlukan
tambahan pekerja. Jika ditulis dalam bentuk tabel adalah sebagai berikut :
|
Pekerja |
Waktu
(Hari ) |
|
20 |
60 |
|
20 |
60-12 = 48 |
|
x |
60-12-8 = 40 |
Jawab :
Note : Semakin sedikit sisa waktu pembangunan rumah tersebut, maka semakin banyak pula pekerja yang dibutuhkan.
Sehingga kita menggunakan rumus perbandingan berbalik nilai.
Jadi, tambahan pekerja yang diperlukan = 24-20 = 4 pekerja. Jawabannya ( A ).
10. Sebuah peternakan mempunyai persediaan makanan selama 24 hari untuk 140 ekor ayam. Jika ayamnya bertambah 20 ekor maka persediaan makanan itu akan habis selama ...hari.
A. 20
B. 21
C. 26
D. 30
Pembahasan :
Diketahui : Banyak ayam setelah ditambah 20 ekor = 140+20 = 160 ekor, jika dalam tabel maka :
|
Waktu ( Hari ) |
Banyak
ayam |
|
24 |
140 |
|
x |
160 |
Jawab :
Note : Semakin banyak ekor ayam, maka semakin cepat pula persediaan makanan akan habis.
Sehingga kita menggunakan rumus perbandingan bebalik nilai.
Jadi, lama persediaan makanan itu akan habis adalah selama 21 hari. Jawabannya ( B ).
Itulah 10 contoh soal perbandingan senilai dan perbandingan berbalik nilai yang sering muncul saat ujian berlangsung. Semoga bisa bermanfaat dan dapat dengan mudah dipahami. Jika ada pertanyaan ataupun ada yang ingin didiskusikan perihal pembahasan soal d atas, tolong tinggalkan pertanyaan di kolom komentar. Tetap semangat dan selalu tebar kebaikan di sekitar kita.
Terimakasih
ReplyDelete