Bilangan berpangkat lengkap dengan sifat dan contoh soal

Pengertian bilangan berpangkat

Suatu bilangan yang dapat dinyatakan dalam bentuk a/b, dengan a dan b merupakan bilangan bulat serta b ≠ 0 dinamakan bilangan rasional

Suatu bilangan yang dapat dinyatakan dalam bentuk a/b, dengan a dan b merupakan bilangan bulat serta b ≠ 0 dinamakan bilangan rasional

Asih pengertian bilangan berpangkat itu?

Bilangan berpangkat adalah jika a bilangan rasional dan n bilangan bulat positif, maka perkalian berulang n faktor dari a adalah a x a x a x...x a (Sebanyak n faktor) dapat ditulis aⁿ atau dapat dinyatakan sebagai :

$\frac{a\times a\times a\times ...\times a}{\text{sebanyak n faktor}}$

Keterangan : a = Bilangan pokok (basis)

n = Pangkat

aⁿ = Bilangan berpangkat

aⁿ = Dibaca a pangkat n

Ada dua bentuk bilangan berpangkat, yaitu :

a. Bilangan berpangkat sebenarnya

adalah bilangan berpangkat yang diperoleh dengan melakukan perkalian berulang.

contohnya yaitu : 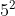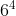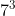$5^{2}$ , $6^{4}$ , $7^{3}$ , dan lain sebagainya.

b. Bilangan berpangkat tak sebenarnya

adalah bilangan berpangkat yang tidak dapat diperoleh dengan perkalian berulang.

contohnya : 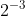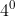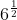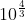$2^{-3}$ , $4^{0}$ , $6^{\frac{1}{2}}$ , $10^{\frac{4}{3}}$ , dan lain sebagainya.

Kita sudah tahu bahwa bilangan berpangkat ada dua bentuk, yaitu bilangan berpangkat sebenarnya ( bialangan berpangkat yang diperoleh dari perkalian berulang ) dan bilangan berpangkat tak sebenarnya ( bilangan berpangkat yang tidak dapat diperoleh dari perkalian berulang ).

Dari kedua bentuk itu, kita mendapat 3 jenis bilangan berpangkat, yaitu jenis bilangan berpangkat bulat positif, jenis bilangan berpangkat negatif, dan juga jenis bilangan berpangkat nol. Berikut penjelasan mengenai tiga jenis bilangan berpangkat tersebut.

1. Bilangan berpangkat bulat positif.

Konsepan pangkat bilangan berawal dari perkalian berulang yang bertujuan untuk meringkas dan menyederhanakan penuliasan perkalian berulang dari bilangan-bilangan dengan faktor-faktor yang sama.

Contoh bilangan berpangkat bulat positif : 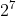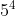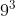$2^{7}$ , $5^{4}$ , $9^{3}$ dan lain sebagainya.

2. Bilangan berpangkat negatif.

Jika a adalah bilangan rasional, a ≠ 0, dan m,n adalah bilangan bulat positif dengan m > n, maka berlaku 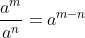$\frac{a^{m}}{a^{n}}=a^{m-n}$

Secara umum, bilangan berpangkat n, dengan n adalah bilangan bulat positif dapat dituliskan sebagai berikut :

$a^{-n}=\frac{1}{a^{n}}\text{ atau }a^{n}=\frac{1}{a^{-n}}$

Contoh bilangan berpangkat negatif :

$4^{-2}=\frac{1}{4^{2}}=\frac{1}{16}$

Dapat kita tarik kesimpulan bahwa definisi dari bilangan berpangkat negatif adalah jika a bilangan rasional, a ≠ 0, dan n adalah bilangan bulat negatif maka ;

$a^{-n}=\frac{1}{a^{n}}$

3. Bilangan berpangkat nol

Bilangan berpangkat nol ini sangatlah unik, karena apa? karena berapapun nilai yang di pangkatkan nol maka semua hasilnya akan 1.

Bilangan berpangkat nol itu sendiri merupakan jika a ialah bilangan rasional, a ≠ 0, dan m,n adalah bilangan bulat positif dengan m = n, maka akan berlaku :

$\frac{a^{m}}{a^{n}}=\frac{a^{m}}{a^{m}}\text{ ( karena m=n )}=a^{m-m}=a^{0}$

Sifat-sifat Bilangan Berpangkat

Setelah mengetahui jenis-jenis bilangan berpangkat itu, maka selanjutnya akan membahas tentang apa saja sifat-sifat yang ada pada bilangan berpangkat dan bagimana cara pengoperasian sifat bilangan berpangkat itu.

Berikut merupakan sifat-sifat bialang berpangkat :

1. Sifat perkalian bilangan berpangkat

Jika a bilangan rasional dan m,n bilangan bulat positif, maka

$\boxed{a^{m}\times a^{n}=a^{m+n}}$

syarat perkalian bilangan berpangkat : ( a ) bilangan pokok harus sama , jika berbeda, maka sifat ini tidak berlaku pada bilangan berpangkat.

Contohnya :

$3^{3}\times 3^{2}=3^{3+2}=3^{5}=243$

2. Sifat pembagian bilangan berpangkat

Jika a bilangan rasional, a ≠ 0, dan m,n bilangan bulat positif, maka

$\boxed{a^{m}:a^{n}=\frac{a^{m}}{a^{n}}=a^{m-n}\text{ dengan }m>n}$

syarat pembagian bilangan berpangkat : ( a ) Bilangan pokok harus sama, jika berbeda, maka sifat ini tidak berlaku pada bilangan berpangkat.

Contohnya :

$\frac{2^{5}}{2^{3}}=2^{5-3}=2^{2}=4$

3. Sifat pangkat bilangan berpangkat

Jika a bilangan rasional dan m,n adalah bilangan bulat positif, maka

$\boxed{\left ( a^{m} \right )^{n}=a^{m\times n}}$

Sifat ini menyatakan bahwa jika suatu bilangan berpangkat dipangkatkan kembali, maka bilangan pangkat itu dikalikan dengan pangkat dari bilangan tersebut.

Contohnya :

$\left ( 2^{2} \right )^{3}=2^{2\times 3}=2^{6}=64$

4. Sifat pangkat dari perkalian bilangan

Jika n bilangan bulat positif dan a,b bilangan rasional, maka

$\boxed{\left ( a\times b \right )^{n}=a^{n}\times b^{n}}$

Perkalian bilangan dengan pangkat bilangan yang sama akan menghasilkan perkalian antara bilangan tersebut dengan pangkat yang sama.

Contohnya :

$\left ( 2\times 3 \right )^{2}=2^{2}\times 3^{2}=4\times 9=36$

5. Sifat pangkat dari pembagian bilangan

Jika a,b bilangan rasional, b ≠ 0, dan n bilangan bulat positif, maka

$\boxed{\left ( \frac{a}{b} \right )^{n}=\frac{a^{n}}{b^{n}}\text{ dengan }b \neq 0}$

Jika ada pembagian bilangan dengan diberi pangkat pada operasian tersebut, maka sama dengan pembagian bilangan dengan masing-masing pangkat yang sama. dengan syarat b≠0.

Contohnya :

$\left ( \frac{2}{5} \right )^{2}=\frac{2^{2}}{5^{2}}=\frac{4}{25}$

6. Sifat pangkat rasional

Jika a bilangan rasional dan m,n bilangan bulat positif, maka

$\boxed{a^{\frac{n}{m}}=\sqrt[m]{a^{n}}}$

Jika ada bilangan yang pangkatnya berupa pecahan, maka hasilnya akan berbentuk akar.

Contohnya :

$3^{\frac{2}{3}}=\sqrt[3]{3^{2}}=\sqrt[3]{9}$

7. Sifat penjumlahan bilangan berpangkat

Konsepan penjumlahan bilangan berpangkat adalah jika a,p,q merupakan bilangan rasional dan m,n adalah bilangan bulat positif, dengan ketentuan m ≥ n maka :

$\boxed{pa^{n}+qa^{m}=a^{n}(p+qa^{m-n})}$

Contohnya :

$3\times 2^{2}+5\times 2^{3}=2^{2}(3+ 5\times 2^{3-2})=2^{2}(3+5\times 2)=4(13)=52$

8. Sifat pengurangan bilangan berpangkat

Konsepan penjumlahan bilangan berpangkat adalah jika a,p,q merupakan bilangan rasional dan m,n adalah bilangan bulat positif, dengan ketentuan m≥n maka :

$\boxed{pa^{n}-qa^{m}=a^{n}(p-qa^{m-n})\\\text{ atau }pa^{m}-qa^{n}=a^{n}(pa^{m-n}-q)}$

Contohnya :

$3\times 2^{2}-6\times 2^{3}=2^{2}(3-6\times 2^{3-2})=2^{2}(3-12)=4(-9)=-36$

Itulah 8 sifat bilangan berpangkat yang wajib temen-temen pahami, ketika kita lupa salah satu sifat bilangan berpangkat ini maka kita akan kebingunan dalam mengerjakan soal bilangan berpangkat. Jadi diharapkan temen-temen bisa mencerna materi ini dengan semaksimal mungkin yah.

Operasi Aljabar yang Melibatkan Bilangan Berpangkat

Pada materi bilangan berpangkat ini kita bisa kaitkan dengan materi aljabar yang telah kita pelajari pada materi sebelumnya.

Kedua materi ini sangat berhubungan erat satu sama lain, sehingga kita perlu mengkolaborasikan sifat-sifat yang ada pada bilangan berpangkat dengan materi aljabar.

Seperti perpangkatan pada suku dua. Berikut contoh perpangkatan suku dua pada aljabar :

( a + b )²= ( a + b ) ( a + b)

= a(a + b) + b(a + b)

= a² + ab + ab + b²

= a² + 2ab + b²

Perpangkatan (a - b)ⁿ juga dapat diselesaikan dengan sifat distributif maupun segitiga pascal. Penyelesaian perpangkatan (a - b)ⁿ dengan segitiga pascal dengan mengubah koefisien pada segitiga pascal dari ( + ) ke ( - ) secara berulang sebgai berikut :

perpangkatan dua suku menggunakan segitiga pascal

Berdasarkan segitiga pascal di atas, Berikut merupakan perpangkatan (a - b)ⁿ.

1. (a - b) ²= a² -2ab + b²

2. (a -b)³ = a³- 3a²b + 3ab² - b³

3. (a - b)⁴= a⁴ - 4a³b + 6a²b² - 4ab³ + b⁴

4. dst...

Jadi, penyelesaian perpangkatan dua suku dapat dengan perkalian distributif maupun segitiga Pascal.

Contohnya :

Tentukan hasil perpangkatan bentuk aljabar (2x + 3)⁴!

Jawab:

(2x - 3)⁴ = 1(2x)⁴ + 4(2x)³(3) + 6(2x)²(3)² + 4(2x)(3)³ + 1(3)⁴

= 16x⁴ + 4(8x³)(3) + 6(4x²)(9) + 4(2x)(27) + (81)

= 16x⁴ + 96x³ + 216x² + 216x + 81

Berikut contoh soal bilangan berpangkat dan pembahasannya.

1. Nilai dari 2² + 2⁴+ 2³. adalah...

Pembahasan :

2² + 2⁴+ 2³ = (2 x 2) + (2 x 2 x 2 x 2 x 2) + (2 x 2 x2)

= 4 + 32 + 8

= 44

2. Nilai dari 2⁴+ 2³

Pembahasan :

2⁴ x 2³ = (2 x 2 x 2 x 2) x (2 x 2 x 2)

= 16 x 8

= 128

3. Bentuk sederhana dari 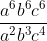$\frac{a^{6}b^{6}c^{6}}{a^{2}b^{3}c^{4}}$ adalah...

Pembahasan :

$\frac{a^{6}b^{6}c^{6}}{a^{2}b^{3}c^{4}}=a^{6-2}.b^{6-3}.c^{6-4}=a^{4}b^{3}c^{2}$

4. Nyatakan dalam bentuk paling sederhana $\left ( \frac{2}{p} \right )^{5}\times \left ( \frac{2}{q} \right )^{-2}$

Pembahasan :

$\left ( \frac{2}{p} \right )^{5}\times \left ( \frac{2}{q} \right )^{-2}=\left ( \frac{2^{5}}{p^{5}} \right )\times \left ( \frac{2^{-2}}{q^{-2}} \right )=\frac{2^{5+(-2)}q^{2}}{p^{5}}=\frac{2^{3}q^{2}}{p^{5}}=\frac{8q^{2}}{p^{5}}$

5. Jika p = q+1 tentukan nilai dari $\frac{(p-q)^{10}\times (p-q)^{7}}{(p-q)^{5}}$ adalah...

Pembahasan :

$\frac{(p-q)^{10}\times (p-q)^{7}}{(p-q)^{5}}=(p-q)^{10+7-5}=(p-q)^{12}$

Selanjutnya kita subsitusikan p = q+1

$(p-q)^{12}=((q+1)-q)^{12}=(q+1-q)^{12}=(1)^{12}=1$

6. Tentukan nilai x dari $27=\left ( \frac{1}{3} \right )^{x}$ adalah...

Pembahasan :

$\\27=\left ( \frac{1}{3} \right )^{x}\\\\3^{3}=\left ( \frac{1}{3} \right )^{x}\\\\\frac{1}{3^{-3}}=\left ( \frac{1}{3} \right )^{x}\\\\\left ( \frac{1}{3} \right )^{-3}=\left ( \frac{1}{3} \right )^{x}\\\\-3=x$

Jadi, nilai x yang memenuhi persamaan di atas adalah -3.

Itulah pembahasan materi mengenai bilangan berpangkat. Semoga bermanfaat dan dapat dengan mudah dipahami oleh temen-temen. Jika ada yang ingin ditanyakan ataupun didiskusikan perihal materi bilangan berpangkat ini, silahkan untuk meninggalkan pesan di kolom komentar. Tidak ada yang tidak mungkin selama batasan antara rasa malas dan logika anda bisa anda kuasai. Tetap bergerkan, salam hangat dari mimin.

Bilangan berpangkat lengkap dengan sifat dan contoh soal

Advertisement

0 Response to "Bilangan berpangkat lengkap dengan sifat dan contoh soal"

Post a Comment