Diketahui kubus ABCD.EFGH dengan panjang rusuk 3 cm. Titik P merupakan perpotongan garis EG dan FH. Nilai sinus sudut antara garis AP dengan bidang BDHF adalah
Diketahui kubus ABCD.EFGH dengan panjang rusuk 3 cm. Titik P merupakan perpotongan garis EG dan FH. Nilai sinus sudut antara garis AP dengan bidang BDHF adalah. . .
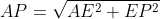
^{2}+(\frac{3}{2}\sqrt{2})^{2}}\\\\=\sqrt{9+\frac{9}{2}}\\\\=\sqrt{\frac{27}{2}}\\\\=\frac{3}{2}\sqrt{6}\text{&space;cm} "\\=\sqrt{(3)^{2}+(\frac{3}{2}\sqrt{2})^{2}}\\\\=\sqrt{9+\frac{9}{2}}\\\\=\sqrt{\frac{27}{2}}\\\\=\frac{3}{2}\sqrt{6}\text{ cm}")
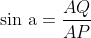
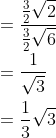
A. 1/2 √3
B. 1/2 √2
C. 1/3√3
D. 1/3 √2
E. 1/4 √2
Pembahasan :
Diketahui :
panjang rusuk = 3 cm
Titik P merupakan perpotongan garis EG dan FH
Ditanyakan : Nilai sinus sudut antara garis AP dengan bidang BDHF adalah. . .?
Jawab :
Kita ilustrasikan soal ke dalam gambar
Dari gambar di atas, proyeksi garis AP pada bidang BDHF adalah garis PQ, sehingga sudut antara AP dengan BDHF adalah <APQ = a.
AC merupakan diagonal sisi, maka AC :
AC = √(AB² + BC²)
= √(3² + 3²)
= √(9 + 9)
= √18
= √((9 x 2)
= 3√2 cm
Karena panjang AQ setengahnya panjang AC, maka :
AQ = 1/2 x AC
= 1/2 x 3√2
= 3/2 √2 cm
Kita telah mengetahui nilai AE = 3 cm dan
EP = AQ = 3/2 √2 cm.
Maka kita cari nilai panjang AP :
Sehingga segitiga APQ siku-siku di Q.
Jadi, nilai sinus sudut antara AP dan BDHF adalah 1/3 √3.
Jawabannya ( C ).
Itulah pembahasan contoh soal mengenai materi bangun ruang kubus yang mimin ambil dari buku detik-setik UNBK 2019. Semoga bermanfaat dan mudah untuk dipahami. Tetap semangat temen-temen, jangan kasih kendor wkwkw. Terima kasih..
0 Response to "Diketahui kubus ABCD.EFGH dengan panjang rusuk 3 cm. Titik P merupakan perpotongan garis EG dan FH. Nilai sinus sudut antara garis AP dengan bidang BDHF adalah"
Post a Comment