Diketahui limas segitiga beraturan T.ABC dengan panjang semua rusuknya 8 cm. Nila cosinus sudut antara TC dan bidang ABC adalah...
Diketahui limas segitiga beraturan T.ABC dengan panjang semua rusuknya 8 cm. Nila cosinus sudut antara TC dan bidang ABC adalah...

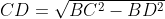
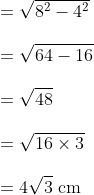

^{2}=(4\sqrt{3})^{2}+8^{2}-2\times&space;4\sqrt{3}\times&space;8.\text{cos&space;}\alpha&space;\\\\(16.3)=(16.3)+64-64\sqrt{3}.\text{cos&space;}\alpha&space;\\\\48=48+64-64\sqrt{3}.\text{cos&space;}\alpha&space;\\\\48-48-64=-64\sqrt{3}.\text{cos&space;}\alpha&space;\\\\-64=-64\sqrt{3}.\text{cos&space;}\alpha&space;\\\\64\sqrt{3}.\text{cos&space;}\alpha&space;=64\\\\\text{cos&space;}\alpha&space;=\frac{64}{64\sqrt{3}}\\\\\text{cos&space;}\alpha&space;=\frac{1}{\sqrt{3}}\\\\\text{cos&space;}\alpha&space;=\frac{1}{\sqrt{3}}\times&space;\frac{\sqrt{3}}{\sqrt{3}}\\\\\text{cos&space;}\alpha&space;=\frac{1}{3}\sqrt{3})
A. 1/2 √2
B. 1/3 √3
C. 1/3
D. 1/2 √2
E. 1/2
Pembahasan :
Diketahui : Panjang rusuk = 8 cm
Ditanyakan : Nilai cosinus sudut antara TC dan bidang ABC adalah...?
Jawab :
* Kita ilustrasikan soal ke dalam bentuk gambar

* Karena titik D berada di tengah antara garis AB, maka panjang BD = 4 cm
* Misalkan sudut antara TC dengan ABC adalah <TCD = a
maka :
TD = CD = 4√3 cm.
* Kita ilustrasikan ke dalam bentuk gambar, maka :

* Kita perhatikan segitiga TCD, pada segitiga di atas berlaku aturan cosinus, maka :
Jadi, nilai cosinus sudut antara TC dan bidang ABC adalah 1/3 √3. Jawabannya ( B ).
Itulah pembahasan soal UN yang mimin ambil dari soal latihan buku detik-detik UNBK atahun 2018. Semoga bermanfaat dan mudah untuk dipahami. Tetap semangat dan jangan mudah berputus asa. Good luckk and thank youu.
0 Response to "Diketahui limas segitiga beraturan T.ABC dengan panjang semua rusuknya 8 cm. Nila cosinus sudut antara TC dan bidang ABC adalah..."
Post a Comment